Кинематика кривошипно-шатунного механизма

Перемещение поршня. Положение поршня определяется отрезком (AA) [рис. 1], определяющимся из выражения:

S_п=r+l-(lcosβ+rcosα).

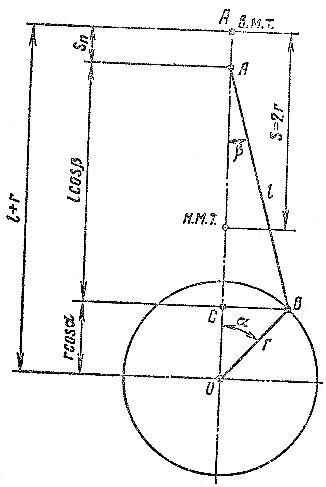
Рис. 1. Схема кривошипно-шатунного механизма.

Из треугольников (OCB) и (ABC) можно записать

rsinα=lsinβ.

Откуда

sinβ=(r/l)sinα=λsinα.

Тогда

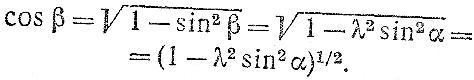
Разложим выражение [(1-λ²sin²α)^1/2] в ряд и, пренебрегая членами выше второго порядка, вследствие их малости, получаем:

cosβ=1-( λ²sin²α/2).

Подставив это в исходное выражение, после преобразования получаем:

S_п=r(l-cosα+(λ/2)sin²).

Полученное выражение является уравнением движения кривошипно-шатунного механизма в зависимости от угла поворота коленвала.

На [рис. 2] представлено графическое изображение перемещения поршня. При α=0, S_п=0 (в.м.т); α=π, S_п=2r (н.м.т.).

Рис. 2. Графики перемещения S_п, скорости ν_п и ускорения j_п поршня в зависимости от угла поворота коленчатого вала.

Скорость поршня. Скорость движения поршня вычисляется путём дифференцирования по времени уравнения движения кривошипно-шатунного механизма:

ν_п=dS_п/dt=( dS_п/dα)•(dα/dt)=r(sinα+( λ/2)sin2α)•(dα/dt),

где (dα/dt)=ω – угловая скорость вращения кривошипа.

ν_п=rω(sinα+( λ/2)sin2α).

График скорости поршня в зависимости от угла поворота коленвала показан на [рис. 2]. При α=0 (в.м.т.) и α=π (н.м.т.) скорость поршня равняется нулю. В (в.м.т) и (н.м.т.) поршень меняет направление движения. Если угол поворота коленвала α=π/2, то ν_п=rω, то есть скорость поршня равна окружной скорости оси кривошипа.

Ускорение поршня. При дифференцировании выражения скорости поршня получается зависимость ускорения от угла поворота кривошипа:

j_п=dν_п/dt=(dν_п/dα)•(dα/dt)= rω(cosα+λcos2α).

Из формулы следует, что ускорение приобретает максимальное значение при α=0 и α=360 град., то есть в в.м.т. При движении поршня минимальное значение ускорения наблюдается в н.м.т.

j_п=-rω²(1-λ).

Общее значение ускорения (как видно из формулы) складывается из пары составляющих:

j_п= j_{п I}+j_{п II},

где rω²cosα=j_{п I} – ускорение первого порядка; rω²cosα=j_{п II} – ускорение второго порядка.

17*