Распределение крутящих моментов между осями (3) [рис. 1, в)] несимметричного дифференциала осуществляется по следующей схеме. В дифференциале имеются двойные конические сателлиты (4). Через шестерню (2) они соединяются с его передней осью, а через шестерню (12) – с задней.
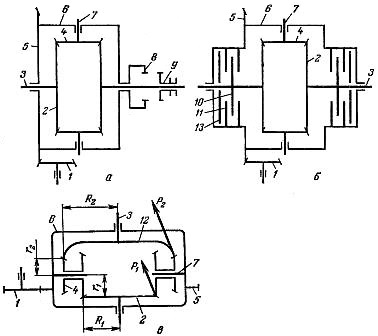
Рис. 1. Схемы дифференциалов.
а) – Схема симметричного блокируемого дифференциала;
б) – Схема симметричного самоблокирующегося дифференциала;
в) – Схема несимметричного дифференциала:
1) – Ведущая шестерня;
2) – Коническая шестерня дифференциала;
3) – Полуось;
4) – Сателлит;
5) – Ведомая шестерня;
6) – Корпус дифференциала;
7) – Крестовина;
8) – Зубцы корпуса;
9) – Зубчатая муфта;
10) – Ведущие диски;
11) – Ведомые диски;
12) – Коническая шестерня дифференциала;
13) – Нажимные чашки.
Из условия равновесия блока сателлитов относительно его оси P1r1=P1r1 либо
P2/P1=r1/r2
* где P1 и r1 – окружное усилие и радиус начальной скорости большего сателлита соответственно, P2 и r2 – то же меньшего сателлита.
Крутящие моменты Мдиф.1 и Мдиф.2, передаваемые передней и задней осям дифференциала соответственно
Мдиф.1=P1R1
Мдиф.2=P2R2
* где R1 и R2 – радиусы начальных окружностей осевых шестерён (2) и (12).
Разделив уравнение (Мдиф.2=P2R2) на уравнение (Мдиф.1=P1R1) с учётом уравнения (P2/P1=r1/r2), получаем
Мдиф.2/Мдиф.1=(r1/r2)•(R2/R1)=iд
* где iд – передаточное число дифференциала.
Мдиф.1+Мдиф.2=Мдиф
* где Мдиф – крутящий момент, подводимый к корпусу дифференциала.
Решая совместно уравнения (Мдиф.2/Мдиф.1=(r1/r2)•(R2/R1)=iд) и (Мдиф.1+Мдиф.2=Мдиф), получаем
Мдиф.1=Мдиф/(1+iд)
Мдиф.2=Мдифiд/(1+iд)
Таким образом, распределение крутящих моментов между осями при несимметричном дифференциале зависит от значения передаточного числа дифференциала (iд). В частном случае, когда r1=r2 и R1=R2 (симметричный дифференциал), iд=1 и Мдиф.1=Мдиф.2.
Симметричный межосевой дифференциал используется в тех случаях, когда сцепные веса обоих ведущих осей одинаковы. В противном случае применяется дифференциал несимметричного типа.
